FiltersDone

Question type

Essay

Multiple Choice

Short Answer

True False

Matching

Exam 13: Multiple Regression Analysis

Show Answer

Share

---

All types

Filters

Study FlashcardsPractice ExamLearn

Question 51

True/False

Review LaterAdd Note

Review Later

In a multiple regression model, the partial regression coefficient of an independent variable represents the increase in the y variable when that independent variable is increased by one unit if the values of all other independent variables are held constant.

A) True
B) False

Correct Answer

verified

Show Answer

Question 52

Multiple Choice

Review LaterAdd Note

Review Later

A market analyst is developing a regression model to predict monthly household expenditures on groceries as a function of family size, household income, and household neighborhood (urban, suburban, and rural) .The "neighborhood" variable in this model is ______.

A) an independent variable
B) a response variable
C) a quantitative variable
D) a dependent variable
E) a constant

F) All of the above
G) B) and D)

Correct Answer

verified

Show Answer

Question 53

Multiple Choice

Review LaterAdd Note

The following ANOVA table is from a multiple regression analysis. $\begin{array} { | c | c | c | c | c | c | } \hline \text { Source } & \mathrm { df } & \mathrm { SS } & \mathrm { MS } & F & p \\\hline \text { Repression } & 3 & 1500 & & & \\\hline \text { Error } & 26 & & & & \\\hline \text { Total } & & 2300 & & & \\\hline\end{array}$ The R² value is __________.

A multiple regression analysis produced the following tables. $\begin{array} { | c | c | c | c | c | } \hline \text { Predictor } & \text { Coefficients } & \text { Stardard Error } & t \text { Statistic } & p \text {-value } \\\hline \text { Irtercept } & 512.2359 & 78.49712 & 7.956176 & 6.88 \mathrm { E } - 06 \\\hline \boldsymbol { x } _ { 1 } & 7.1525 & 1.652255 & 5.186319 & \mathbf { 0 . 0 0 0 3 0 1 } \\\hline \mathbf { x } _ { 2 } & \mathbf { 2 . 0 2 0 8 } & 0.699194 & 6.774248 & \mathbf { 3 . 0 6 E - 0 5 } \\\hline\end{array}$ $\begin{array} { | c | c | c | c | c | c | } \hline \text { Source } & \mathrm { df } & \text { SS } & \text { MS } & F & p \text {-value } \\\hline \text { Repression } & 2 & 1660914 & \mathbf { 8 3 0 4 5 7 . 1 } & 58.31956 & 1.4 \mathrm { E } - 06 \\\hline \text { Residual } & 11 & 156637.5 & 14239.77 & & \\\hline \text { Total } & 13 & 1817552 & & & \\\hline\end{array}$ If x₁= 25 and x₂ = 85, then the predicted value of y is ____________.

Regression analysis with two dependent variables and two or more independent variables is called multiple regression.

The following ANOVA table is from a multiple regression analysis. $\begin{array} { | c | c | c | c | c | c | } \hline \text { Source } & \mathrm { df } & \mathrm { SS } & \mathrm { MS } & F & p \\\hline \text { Repression } & 3 & 1500 & & & \\\hline \text { Error } & 26 & & & & \\\hline \text { Total } & & 2300 & & & \\\hline\end{array}$ The MSE value is closest to__________.

In the model y = $\beta$ ₀ + $\beta$ ₁x₁ + $\beta$ ₂x₂ + $\beta$ ₃x₃ + $\varepsilon$ , $\varepsilon$ is a constant.

A multiple regression analysis produced the following tables. $\begin{array} { | c | c | c | c | c | } \hline \text { Predictor } & \text { Coefficients } & \text { Stardard Eror } & \boldsymbol { t } \text { Statistic } & p \text {-value } \\\hline \text { Irtercept } & 616.6849 & 154.5534 & 3.990108 & 0.000947 \\\hline \boldsymbol { x } _ { 1 } & - 3.33833 & \mathbf { 2 . 3 3 3 5 4 8 } & - 1.43058 & \mathbf { 0 . 1 7 0 6 7 5 } \\\hline \mathbf { x } _ { 2 } & 1.780075 & \mathbf { 0 . 3 3 5 6 0 5 } & 5.30407 & 5.83 \mathrm { E } - 05 \\\hline\end{array}$ $\begin{array} { | c | c | c | c | c | c | } \hline \text { Source } & \mathrm { df } & \text { SS } & \text { MS } & F & p \text {-value } \\\hline \text { Repression } & 2 & 121783 & 60891.48 & 14.76117 & 0.000286 \\\hline \text { Residual } & 15 & 61876.68 & 4125.112 & & \\\hline \text { Total } & 17 & 183659.6 & & & \\\hline\end{array}$ These results indicate that ____________.

A multiple regression analysis produced the following output from Excel. 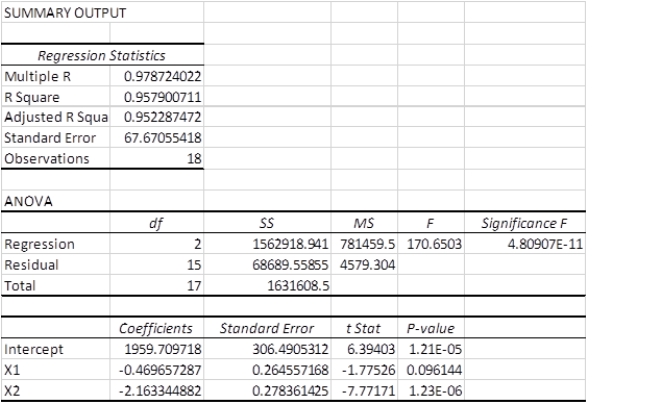The correlation coefficient is ____________.

The following ANOVA table is from a multiple regression analysis. $\begin{array} { | c | c | c | c | c | c | } \hline \text { Source } & \mathrm { df } & \mathrm { SS } & \mathrm { MS } & F & p \\\hline \text { Repression } & 3 & 1500 & & & \\\hline \text { Error } & 26 & & & & \\\hline \text { Total } & & 2300 & & & \\\hline\end{array}$ The observed F value is __________.